Papier wszystko przyjmuje - o poprawę edukacji przez zadania, cz. I

Artykuł ten po raz pierwszy ukazał się w grudniu 2016 roku w Antocyjanie. W zwiazku z tworzeniem bazy zadań-bubli uważam, że trzeba go przypomnieć. Jednocześnie zaznaczam, że część wymienionych poniżej zadań nie jest obecna w nowszych edycjach zbioru zadań, z którego korzystałem pisząc ten artykuł przed laty. Ale problem nie zniknął - podobne zadania do omówionych poniżej znajdują się nadal w innych zbiorach. Dlatego na fotografii, choć cytowane zadania z nich nie pochodzą - są różne dostępne obecnie zbiory. Po prostu tego typu zadania nadal są w "obiegu".

Bezcenne było kiedyś na maturalnej grupie dyskusyjnej zobaczyć kłótnię maturzystów o to, jaką gęstość ma aceton: mniejszą czy większą niż gęstość wody? Jedni pisali, że mniejszą, a drudzy, że większą. Skąd wynikła ta kłótnia? Jedni sugerowali się jednym zadaniem z pewnego zbioru zadań, inni innym zadaniem, ale z tego samego zbioru zadań! Jak w ogóle jest możliwe, że doszło do takiej kłótni? (dodane 23.02.2024)

Ten artykuł chcę skierować nie tylko do osób uczących się czy studiujących, ale też do osób związanych z edukacją chemiczną. Ma to być forma apelu, nie tylko do nauczycieli, co i do autorów zbiorów zadań, bo to także osoby związane z edukacją. Chcę tym razem zwrócić uwagę na pewne niuanse obecne w zbiorach zadań. Papier przyjmuje wszystko, ale czy ilość zawsze wiąże się z jakością? Chciałbym poruszyć tutaj kilka problemów edukacyjnych. Jak wiemy, nieodzownym elementem edukacji są ćwiczenia: obliczeniowe, sprawdzające wiedzę czy też umiejętność jej wykorzystania w praktyce.  W związku z tym na rynku szkolnym dostępnych jest obecnie wiele zbiorów zadań, zwłaszcza przygotowanych pod katem rozszerzonej matury, a poszczególne wydawnictwa ze sobą konkurują, a nawet reklamują się bardzo populistycznymi hasłami. Co gorsze, książki te są często bezkrytycznie zalecane uczniom. Czy jednak ilość zadań w zbiorach idzie w parze z jakością kształcenia? Zaraz się przyjrzymy i wspólnie poszukamy odpowiedzi na pytanie, czy aby na pewno. 
Oczywiście nie ma ludzi niepopełniających błędów – sam nieraz napisałem coś, co potem prostowałem po głębszym przemyśleniu lub własnym dokształceniu się, bowiem wychodzę z założenia, że człowiek uczy się przez całe życie. Zapewne wszyscy nauczyciele zdają sobie też sprawę z tego,  że zadania obliczeniowe niekoniecznie muszą mieć pełne pokrycie z praktyką laboratoryjną, jednak ułańska fantazja autorów nie powinna zbyt mocno wkraczać na łono edukacji, jeśli ma przynieść wymierne korzyści. Pamiętajmy, że odbiorcami są przecież ludzie, którzy dopiero pewne umiejętności i wiedzę zdobywają – powinny docierać więc do nich zadania takie, które nie namieszają im w głowach, pozwolą wysnuć prawidłowe wnioski, obeznać się z danym zagadnieniem, nie wypaczyć ich edukacji. Czy tak jest faktycznie? Pozwoliłem sobie wyłuszczyć dostrzeżone dość regularnie powtarzające się nieprawidłowości w zbiorach zadań. Są one dość wspólne dla zbiorów, ale w jednych coś jest bardziej sporadyczne, a w innych niestety wręcz nagminne. Można odnieść nawet wrażenie, że zadania tworzone są na zasadzie byle tylko jakieś były. Spróbujmy sobie odpowiedzieć teraz na pytanie: komu i czemu ma służyć taki stan rzeczy? Dalszą konsekwencją powinno być poszukiwanie odpowiedzi na kolejne pytanie: czy ktokolwiek sprawuje pieczę nad tym, co pojawia się na rynku szkolnym? Czy ktokolwiek bierze za to odpowiedzialność, weryfikuje treści przeznaczone do publikacji w celach edukacyjnych? Czy też może panuje pełna swoboda, a nikt nie weryfikuje, czy praca została wykonana rzetelnie?

Z góry podkreślam – pojedyncze pomyłki są dla mnie całkowicie normalne – każdy może się pomylić. Zapewne dla każdego takie rzeczy są całkowicie normalne, ale sytuacje, gdy całe zestawy zadań oparte są na błędnych założeniach, dają prawo mieć  pretensje do  ich autora, od którego jednak oczekuje się pewnej rzetelności pracy. Ze względu na obszerność tematu postanowiłem go podzielić na części. Dziś skupimy się bardziej na matematyce, następnym razem bardziej na właściwościach chemicznych.

1. Gęstość rozpuszczalników

Przyjrzyjmy się fragmentom poleceń do zadań związanych z obliczeniami procentowymi:
„W 200 cm³ etanolu o gęstości 1,8 g·cm^-3”
„Oblicz, w jakiej objętości etanolu o gęstości 0,95 g·cm^-3”
„Do przygotowania spirytusu salicylowego użyto 12,9 dm³ etanolu o gęstości 0,76 g·cm^-3”
Wszystkie te cytaty pochodzą z sąsiednich zadań z jednego zbioru. Tablicowe wartości podają gęstość etanolu jako 0,789 g·cm^-3 w 20 °C. O ile wartość 0,76 nie budzi większych zastrzeżeń, o tyle wartość 0,95 jest już zastanawiająca – czy chodzi o etanol, czy też o jego niezbyt stężony wodny roztwór, który także możemy zwać etanolem, lub po prostu alkoholem, tak jak np. wódkę? Ale wartość 1,8? Przecież butelka spirytusu i butelka st. kwasu siarkowego (1,84 g·cm^-3 w temp. pokojowej) mają zupełnie różne masy. Tylko o kwasie siarkowym mówimy, że jest to ciężka ciecz. Spójrzmy na kolejne zadanie:
„35 g substancji organicznej rozpuszczono w 0,4 dm³ acetonu o gęstości 1,1 g·cm^-3”

Wszystkie te cytaty pochodzą z sąsiednich zadań z jednego zbioru. Tablicowe wartości podają gęstość etanolu jako 0,789 g·cm^-3 w 20 °C. O ile wartość 0,76 nie budzi zastrzeżeń, o tyle wartość 0,95 jest już zastanawiająca – czy chodzi o etanol, czy też o jego niezbyt stężony wodny roztwór, który także możemy zwać etanolem, lub po prostu alkoholem, tak jak np. wódkę? Ale wartość 1,8? Przecież butelka spirytusu i butelka st. kwasu siarkowego (1,84 g·cm^-3 w temp. pokojowej) mają zupełnie różne masy. Tylko o kwasie siarkowym mówimy, że jest to ciężka ciecz. Spójrzmy na kolejne zadanie:

„35 g substancji organicznej rozpuszczono w 0,4 dm³ acetonu o gęstości 1,1 g·cm^-3”

Tablice podają gęstość acetonu 0,785 g·cm^-3 w temperaturze 20 °C. Aceton jest więc lżejszy od wody. Z jeszcze innego zadania umieszczonego pomiędzy poprzednimi dowiadujemy się, że jodyna, oparta przecież na alkoholu, ma gęstość 0,8 g·cm^-3… Tak więc etanol ma mieć gęstość nawet 1,8, ale jodyna z niego otrzymana tylko 0,8? Rodzi to więc pytanie, czy autorzy biorą pod uwagę rzeczywistość, czy też wpisują wartości jakie tylko im przyjdą na myśl.? I jaki jest cel dydaktyczny takiego podejścia? Przyjrzyjmy się następnym kwestiom.

2. Jaką objętość mają roztwory? 

Czy jeśli zmieszam litr wody z litrem spirytusu to otrzymam mniej niż litr wódki? Zapewne nie. Roztwory mają zawsze większą objętość niż objętość pojedynczego składnika i bliską sumie objętości składników, czyli otrzymam ok. 2 litry wódki w wyniku mojej czynności. Przyjrzyjmy się jednak zadaniom, na które są skazani przygotowujący się do matury. Przyjrzyjmy się na początek tym poleceniom:
„11,1 g chlorku wapnia rozpuszczono w 300 cm³ wody (gęstość wody 1 g·cm^-3) otrzymując r-r o gęstości    1,5 g·cm^-3”        
„Roztwór kwasu solnego o gęstości 1,4 g·cm^-3 uzyskano rozpuszczając 1,11 dm³ chlorowodoru (warunki normalne) w 400 cm³ wody (gęstość wody 1 g·cm^-3)”
„Rozpuszczono 2,24 dm3 amoniaku w 0,5 dm³ wody otrzymując roztwór o gęstości 1,35 g·cm^-3”
„Wykonaj obliczenia, za pomocą których ustalisz stężenie molowe roztworu metanalu w 35% roztworze formaliny (roztwór metanalu HCHO), o gęstości 1,97 g·cm^-3”
Teraz pamiętajmy, że roztwór ma zawsze objętość zbliżoną do sumy objętości jego składników. Zbliżoną, że względu na kontrakcję, czyli zmniejszenie objętości w stosunku do sumy objętości składników. Ale nigdy roztwór nie może mieć objętości mniejszej niż objętość samego rozpuszczalnika, czy któregokolwiek innego składnika użytego do otrzymania tego r-ru. Pozwoliłem sobie zebrać wyniki w tabeli:

*dla substancji gazowych przyjęto warunki normalne oraz, że zachowują się jak gazy doskonałe

Duża liczba przy sumie objętości   w przypadku HCHO nie powinna dziwić. Gazy ze względu na duże odległości pomiędzy cząsteczkami lub atomami zajmują wielokrotnie większą objętość     niż uzyskane w wyniku ich skroplenia ciecze. Gdyby skroplić  402 dm³ (warunki normalne) metanalu, zajmował by objętość mniejszą niż objętość  1 dm³, bo ok. 630 ml, a suma objętości składników wynosiła by ok. 1630 ml. Widzimy więc, że nie ma znaczenia, czy rozpuszczamy w wodzie gaz, czy ciecz – objętość r-ru zawsze jest większa niż objętość rozpuszczalnika – przecież substancja rozpuszczona też zajmuje jakąś objętość. Czasem spotykam się z pytaniami osób korzystających ze zbiorów zadań – dlaczego objętość roztworu jest mniejsza, niż objętość użytego rozpuszczalnika? I tutaj mamy do popisu jeśli chodzi o uzasadnienie tego: no przecież kontrakcja. Kontrakcja towarzyszy np. mieszaniu wody i etanolu i wynosi ok. 3% w przypadku zmieszania tych samych objętości. Oznacza to jednak, że objętość r-ru będzie o ok. 3% mniejsza od SUMY objętości składników, a nie od objętości samego rozpuszczalnika, bo byłby to taki paradoks, że mieszając   1 dm³ wody z 1 dm³ czystego etanolu otrzymali byśmy mniej niż 1 dm³ wódki… Ale za to bardzo ciężkiej, bo miałaby gęstość kwasu siarkowego. Kontrakcję bardzo dobrze widać np. w przypadku r-ru chlorku wapnia, z wyżej przytoczonych przykładów. Dlaczego więc autorzy sugerują, że r-ry mają mniejszą objętość. Autorzy sugerują też, roztwór kwasu o stężeniu 0,44% ma gęstość wyższą niż stężony kwas (38% ma gęstość 1,19 g/cm³)  - a przecież  uczniowie często bardzo dobrze pamiętają jaką gęstość mają stężone kwasy. Powinni też zdawać sobie sprawę z tego, że roztwory o niskim stężeniu mają właściwości zbliżone do właściwości czystego rozpuszczalnika, czyli w tym przypadku wody.   Oprócz tego typu niedopatrzeń spotykamy także zadania będące w sprzeczności z poprzednimi. Przyjrzyjmy się zadaniu poniżej:

„Z dokładnością do jednego miejsca po przecinku oblicz stężenie molowe 20% r-ru kwasu solnego o gęstości 1,45 g·cm^-3”
Zastanówmy się nad tym paradoksem: woda ma gęstość 1 g·cm^-3, kwas o stężeniu 0,44% - 1,4, a kwas 20% - 1,45. Skąd tak wielki skok gęstości przy przejściu z wody (0% HCl) do 0,44%, a tak mały przy zmianie stężenia z 0,44 do 20%?Czyli gdy stężenie roztworu wzrasta aż 45 razy, to gęstość zmienia się juz tylko 0,05 g/cm³. Ponadto jak wyjaśnić fakt, że kwas o stężeniu 0,44% ma wyższą gęstość od kwasu stężonego (1,19 g/cm³). Czy rozpuszczaniu gazowego chlorowodoru w wodzie towarzyszy jakiś gwałtowny skurcz objętości powstającego roztworu, a następnie rozkurcz w miarę wzrostu stężenia? Na pewno nie, a takie m.i. wnioski można by z tego wysnuć.   Spójrzmy jeszcze na kolejne przykłady:

„Jaka jest gęstość 10% roztworu kwasu siarkowego (VI) o stężeniu 1 mol·dm^-3? 
„Oblicz stężenie procentowe kwasu siarkowego (VI) o stężeniu   0,5 mol·dm-3 i gęstości 1,78 g·cm^-3”
Pamiętamy zapewne, że woda ma gęstość w przybliżeniu równa 1 g/cm³, a st. kwas siarkowy(VI) 1,84 g/cm³.   Z zadania powyżej dowiadujemy się, że jednomolowy kwas (czyli o stężeniu 1 mol/dm³) ma gęstość 0,98 g/cm³, a zatem mniejszą od gęstości rozpuszczalnika! Za to kwas półmolowy (tzn. o stężeniu 0,5 mol/dm³) ma gęstość bliską stężonego kwasu siarkowego, który jest w przybliżeniu 18-stomolowy? Jakby to wyglądało na wykresie? Spójrzmy więc. 

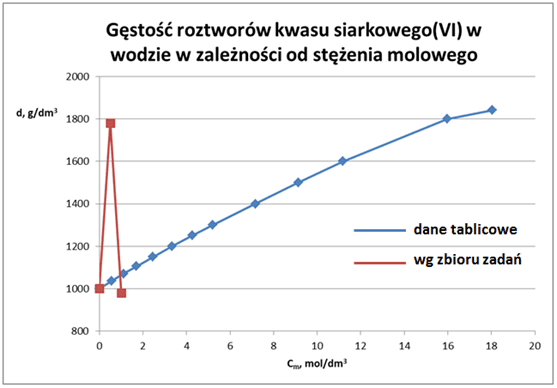
Ale już nie tylko o ten wykres chodzi... No wyobraźmy sobie, że mamy rozcieńczyć kwas o stężeniu 1 mol/dm³ do 0,5 mol/dm³. Co trzeba zrobić? Zwiększyć jego objętość 2 razy. Czyli np. z 1 dm³ kwasu bardziej stężeonego zrobić 2 dm³ kwasu bardziej rozcieńczonego. Wychodzi na to, że powinniśmy do bardziej stężonego kwasu dodać ok. 1 dm³ czystej wody, żeby otrzymać 2 dm³. No dobrze, tylko że ten rozcieńczony kwas ma mieć gęstość 1,78 g/cm³, a więc 2 dm³ będą ważyć 3,56 kg... A to oznacza, że aby z 1 litra (czyli 1 dm³) zrobić 2 dm³ to trzeba dodać 3,56 - 0,98 = 2,58 kg wody, czyli 2,58 litra. Czaimy bazę? Żeby z 1 litra zrobic 2 litry trzeba dolać nie litr wody, tylko 2,58 litra wody! To przecież nie nie ma sensu!

Niestety z powodu braku odpowiednich zadań nie można wykreślić stężenia dalej za 1 mol/dm³, ale biorąc pod uwagę inwencję autorów jej przebieg powinien być ciekawy.  Możemy sobie policzyć, że wg sugestii autorów aby otrzymać 1 dm³ półmolowego kwasu, 1,731 dm³ wody… Gdybyśmy jeszcze chcieli porównać rzeczywistość z zadaniami liczonymi przez uczniów to w przypadku kwasu solnego, to otrzymamy taki widok:

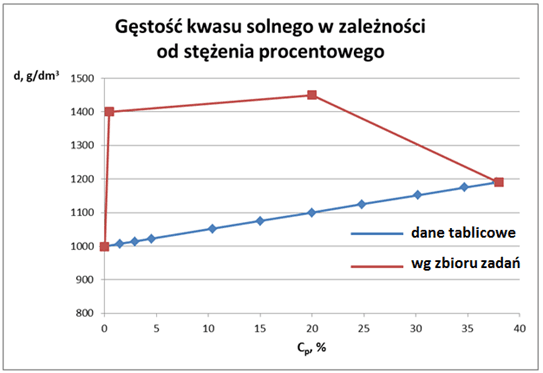
Tutaj również rozpuszczaniu HCl początkowo towarzyszy gwałtowny skurcz objętości… Ale potem już rozkurcz, bo gęstość spada. Podobne sprzeczności można znaleźć w zadaniach z innymi związkami, np. dowiemy się, że  10% r-r NaOH jest równocześnie r-rem o stężeniu 4 mol/dm3, ale już z sąsiedniego zadania wynika, że 3 mol/dm³. 

3) Warunki normalne – co to właściwie znaczy?
W jednym z poprzednich artykułów wspomniałem o zamieszaniu, które ma miejsce z związku z warunkami normalnymi, standardowymi oraz stanem standardowym, który często mylnie jest określany warunkami standardowymi. Jednakże tym razem chciałem zwrócić na coś zupełnie innego. Na nadużywanie tego pojęcia w sposób co najmniej dziwny. Wiemy, że warunkami normalnymi umownie posługujemy się w przypadku obliczeń związanych z gazami, oraz że molowa objętość substancji gazowych wynosi ok. 22,4 dm³. Około, bo gazy rzeczywiste zachowują się w sposób zbliżony do gazu doskonałego, ale nie są zupełnie jak gaz doskonały, więc  obserwuje się pewne odchylenia od tej wartości. Ale do rzeczy. Substancje mają różny stan skupienia w warunkach normalnych. I tak woda w warunkach normalnych może być zarówno cieczą jak i ciałem stałym, bo to jest temperatura równowagi fazowej ciecz-ciało stałe. Siarka jest w warunkach normalnych ciałem stałym. Amoniak występuje w warunkach normalnych w stanie gazowym. Objętość substancji gazowych podajemy zazwyczaj w przeliczeniu na objętość zajmowaną w warunkach normalnych. Jednakże nie wszystko w warunkach normalnych jest gazem. Gdyby woda była w warunkach normalnych gazem, to zajmowała by objętość ok. 22,4 dm³. Ale nie jest gazem, a cieczą lub nawet ciałem stałym, nad którymi może istnieć para wodna. Pytanie więc, jaką objętość zajmie para wodna pod odparowaniu 1 mola wody w warunkach normalnych? Odpowiedź: 3784 dm³. Dlaczego? Dlatego, że tylko substancje o prężności pary nasyconej >1013 hPa zajmą objętość 22,4 dm³. Woda osiąga prężność pary nasyconej 1013 hPa dopiero w 100 °C. W warunkach normalnych osiąga ona ciśnienie (prężność) par tylko 6 hPa. Ciśnienie otoczenia nie ma wpływu na prężność pary nasyconej. Z równania stanu gazu doskonałego możemy policzyć, że objętość molowa pary wodnej wynosi blisko 4 m³. W temperaturze 20 °C to nieco ponad 1 m³, bo rośnie ciśnienie pary nasyconej. Co by się stało, gdybyśmy zaczęli sprężać parę nasyconą? Po prostu by się skropliła i ciśnienie wróciło by do początkowej wartości 6 hPa. Po prostu aby odparować całkowicie 1 mol wody w temperaturze 0 °C to zarówno w próżni jak i w powietrzu pod ciśnieniem 1013 hPa potrzebujemy 3784 dm³ dostępnej przestrzeni. Z tego też powodu potrzebujemy czasem otworzyć drzwi i okno, by wyschła umyta podłoga. Wróćmy jednak do rzeczy. Przyjrzyjmy się fragmentom poleceń:
„Jaką objętość zajmie para kwasu octowego w warunkach normalnych powstała przez odparowanie 60 g kwasu octowego w warunkach normalnych?”
I z odpowiedzi wynika, że kwas octowy w warunkach normalnych jest gazem. Jest tyle związków, które w warunkach normalnych mogą występować jako gaz, czy nie można by wybrać np. NH₃ – przecież 1 mol amoniaku po odparowaniu w warunkach normalnych zajmie objętość 22,4 dm³ Spójrzmy na inne zadanie:
„Z ilu atomów składa się cząsteczka siarki w postaci pary jeżeli gęstość par siarki w warunkach normalnych wynosi 11,43 g·cm^-3?” 
Czy siarka w warunkach normalnych jest parą? Nie, jest ciałem stałym, które posiada jakąś prężność par nad sobą. Nie jest możliwe by posiadała taką gęstość par, jaką podaje się w treści, bo jej gęstość ogranicza ciśnienie pary nasyconej. Tymczasem siarka osiąga prężność par 1013 hPa w 444 °C, a 1 hPa dopiero w 102 °C. W warunkach normalnych ilość par siarki jest minimalna, bo jej prężność wynosi znacznie poniżej 1 hPa ( a wody 6 hPa). Tutaj też pytanie do autora zadania, czy nie można było dokonać szczęśliwszego wyboru, albo zmodyfikować polecenie. 
Odpowiedzmy sobie jeszcze raz na pytanie: po co używamy warunków normalnych? Po to by ułatwić sobie życie, gdyż w laboratoryjnej rzeczywistości raczej pracujemy w temperaturach 20-25 °C i pod ciśnieniem ok. 1000 hPa. Umownie podajemy objętość gazów w przeliczeniu na warunki normalne, by sobie i innym ułatwić obliczenia: objętość podaną w przeliczeniu na warunki normalne możemy bezpośrednio zamienić na liczbę moli czy na masę gazu. Np. mierzymy objętość wydzielonego CO₂ – sprawdzamy jaka jest temperatura i ciśnienie danego dnia w laboratorium, przeliczamy tę objętość na warunki normalne i dalej liczy się już bardzo wygodnie. Ale zwróćmy uwagę na użyty zwrot: w przeliczeniu na. Objętość substancji, która w warunkach normalnych jest gazem zawsze możemy podawać w przeliczeniu na nie. Ale co w przypadku np. wody czy siarki, które w warunkach normalnych gazami nie są, a jedynie posiadają pewne ciśnienie par nad sobą? Można przeliczyć na warunki normalne, bo to w końcu tylko matematyka, np. można obliczyć jaką gęstość miałaby para wodna w warunkach normalnych, gdyby się nie skropliła podczas sprężania z 6 do 1013 hPa. Zatem moglibyśmy podać gęstość par siarki czy wody w przeliczeniu na warunki normalne, ale nei w warunkach normalnych, bo te substancje gazami w tych warunkach nie są. Po prostu zakładamy co by było, gdyby. Wydaje, że to tylko kosmetyczny błąd, jednak ma spore konsekwencje  –  po co wypaczać uczącym się ludziom myślenie w taki sposób, że mogą zacząć myśleć, że mol pary wodnej zajmuje objętość 22,4 dm³ w warunkach normalnych? Przecież woda byłaby gazem w tych warunkach.

Sensem edukacji poprzez zadania rachunkowe powinien być cel: poukładać sobie wiadomości poprzez policzenie zadań, a tymczasem można im namieszać w głowach. To chyba nie o to chodzi, by liczyć zadania z automatu, nie wiedząc co się liczy, a jak widzę wśród ludzi z którymi mam do czynienia – często liczą jak roboty, bez zastanawiania się czy to ma jakiś sens. Czy to jest sensem edukacji?  Na tym proponowałbym zakończyć pierwszą część artykułu. Następnym razem skupimy się na pojęciu wydajności reakcji, oraz na zadaniach opartych o właściwości substancji, których one nie posiadają. Apeluję do autorów, by trochę większą uwagę zwracali nie tylko na to ile piszą, ale też co piszą. Apeluję także do nauczycieli, by także zwracali na takie niuanse większą uwagę i wyjaśniali to, co zostało użyte w nieodpowiednim znaczeniu albo, że to tylko matematyka i wynik nie ma nic wspólnego z rzeczywistością, bo po prostu autor dane sobie wymyślił bez weryfikacji ich z tablicami. 

A sensem edukacji nie jest chyba to, by wypełnić czymś młodzieży 45 min lekcji, oraz popołudnia po szkole, tylko coś im przekazać i czegos ich nauczyć... Ale czy jest tak jak powinno być?

Druga część artykułu znajduje się tutaj (kliknij).