Tym razem rozpatrzymy to zadanie:

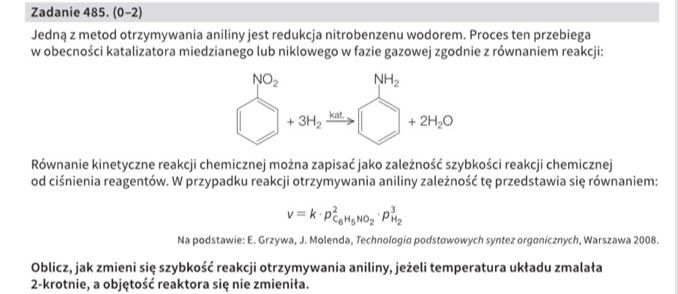
I rozwiązanie zaproponowane przez wydawnictwo:

Czy rozwiązanie to ma jakiś sens? Niestety, ale autor zapomniał o jednej, bardzo istotnej rzeczy. 

Ciśnienie gazu jest ekwiwalentem jego stężenia, Co wynika z faktu, 
Ciśnienie gazu jest ekwiwalentem jego stężenia, co wynika z faktu, że ciśnienie zależy od liczby cząsteczek w danej objętości. A więc od stężenia gazu.
 

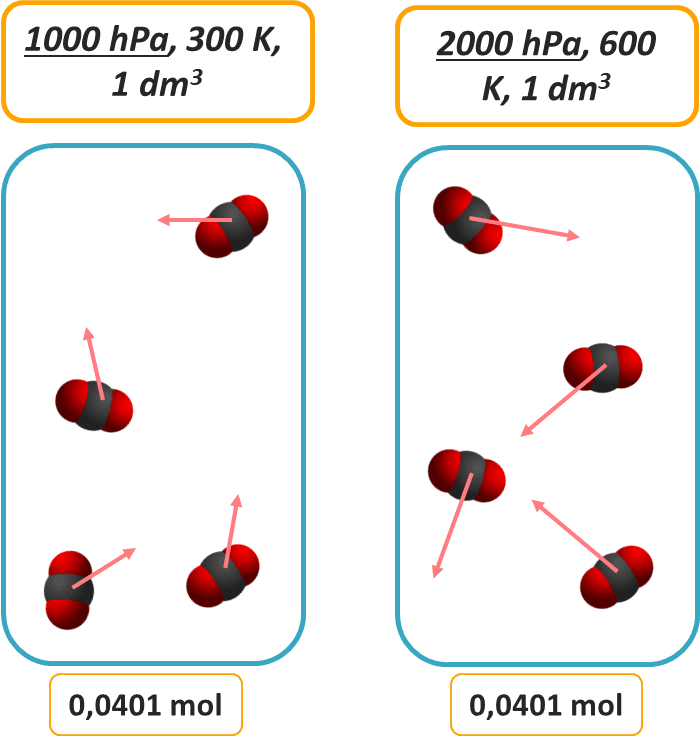
Stężenie gazu w drugim naczyniu o tej samej objętości jest 2 razy wyższe, bo jest w nim 2 razy więcej cząsteczek gazu. Jest tylko jeden szkopuł. Ta zasada pracuje, gdy mówimy o tej samej temperaturze. Dlatego, że ciśnienie gazu zależy także od temperatury. Wyższej temperaturze cząsteczki gazu poruszają się szybciej, a więc częściej i mocniej uderzają o ścianki naczynia. Nawet jeśli jest ich tyle samo, to w wyższej temperaturze wywierają wyższe ciśnienie.

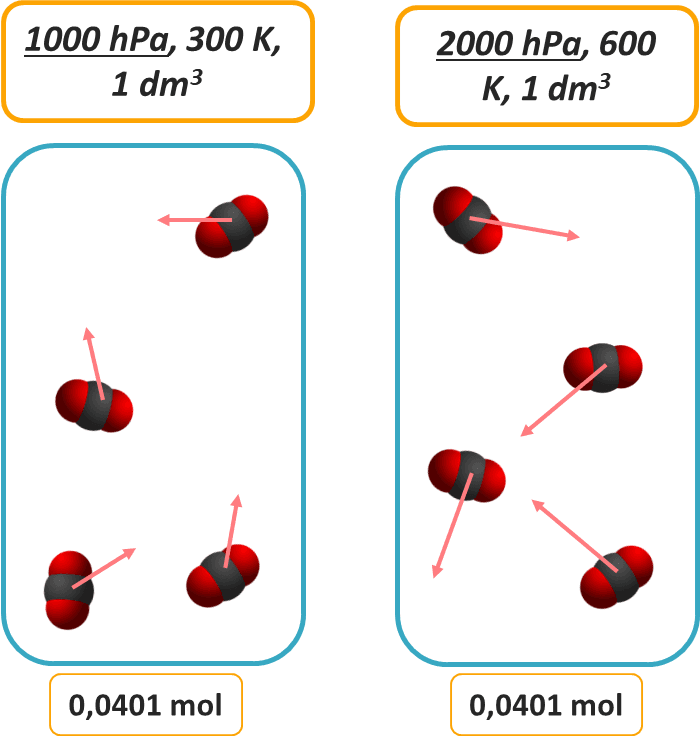
Przyjrzyjmy się, że w obu naczyniach stężenie będzie takie samo: 0,0401 mol/dm³. Obniżenie więc temperatury o połowę np. 600 K do 300 K Spowoduje dwukrotny spadek ciśnienia, ale nie stężenia.

Szybkość reakcji rzeczywiście spadnie. Ale nie ma to w związku ze spadkiem stężenia, tylko ze spadkiem temperatury, przez co cząsteczki będą się poruszać wolniej. A więc rzadziej będą się zderzać i reagować za sobą wobec tego. Wpływ temperatury na szybkość reakcji określamy za pomocą współczynnika temperaturowego tej reakcji lub dokładniej za pomocą znacznie lepiej opsujacego rzeczywistość równania Arrheniusa. Równanie Arrheniusa opisuje w jaki sposób stała szybkości reakcji zależy od temperatury.